2025年の8月2日に実施された京都大学情報学研究科
社会情報学コースの大学院試験 基礎科目の解説です。
基礎科目はアルゴリズムを問う問題が多くて解いてて楽しいので解きました。
これから受験する人の参考になったら嬉しいです。
回答内容についてはあくまで私の回答なので、参考程度にしてください。
どうしても修正したい点があるならプルリクしてください。
マシン語は限られた条件や操作でいかにアルゴリズムを実装するかが問われる問題です。 できる操作が限られるので、プリミティブに考えることが大事なのかなと思っています。 試験におけるコツとしては最後まで諦めずに手法を考え続けることだと思います。 ふと解き方が浮かんできたりします。
自然数MとNの大小比較を行う問題です。高級な言語ならif文で一発ですが、マシン語ではそうはいきません。
私が思いついた解法はレジスタ0に格納した値を1ずつインクリメントし、その度にJunp命令を用いて
MとNに一致するかを判定します。これにより、レジスタ0の値がMに先に一致した場合はMの方が小さい、
レジスタ0の値がNに先に一致した場合はNの方が小さいと判断できます。
また、これだけでは大小判定しかできないので、レジスタ0の値がMと一致した際にはNと一致するかも判定し、
M=Nであるかの判定を行います。
ロード命令が4回までしか実行できないので、おそらくこのやり方になると思います。
(最初にN=Mの判定をしているとロードの回数が足りなくなりました)
この問題の仮定として、レジスタの初期値が0であることが仮定されていません。
レジスタに0を格納するためには最初はロードを用いますが、そのあとは
add命令を用いて0+0=0を指定レジスタに格納という手法を用います。
レジスタ0の値のインクリメントのループを作るためにはjump命令を用います。
jump命令の実行時にレジスタ0とレジスタ0の値の比較を行うことにより、必ずジャンプする処理を実装できます。
これによりループ命令を実装します。
以下がアルゴリズムの実装のフローです。
すみません、、さすがにマシン語まで書くのはしんどいので、割愛します。
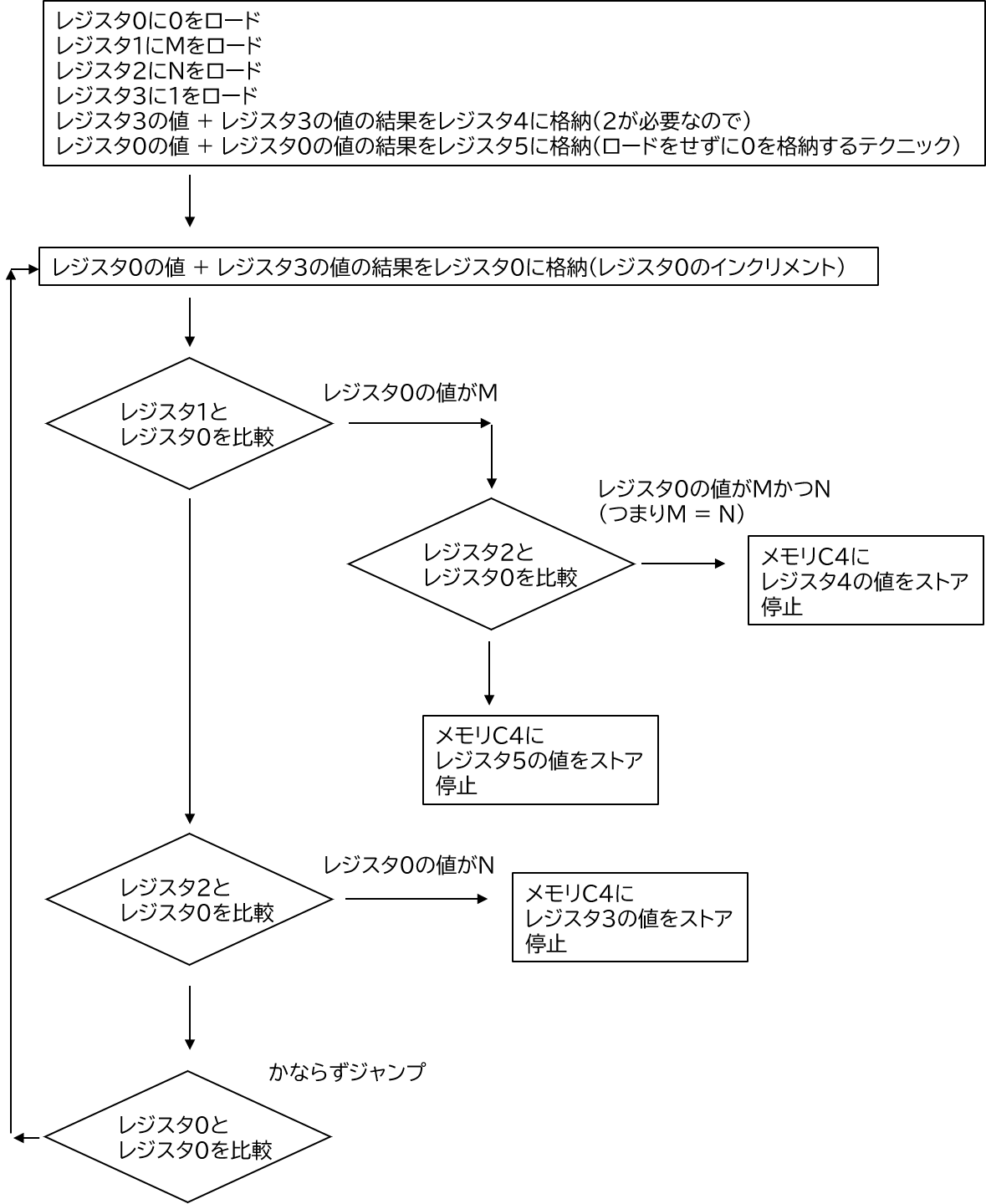
この問題を考える際の考え方の道筋は、まず分岐の実装はjump命令を使うしかないということです。 そのため使える判定はレジスタ0との値が同じかどうかということです。 そのため、大小の比較ではなく、値が同じかどうかという処理を基準に解法を検討します。 そして次のヒントはM,Nが255までの数字ということです。 8bitにおいては255が上限であることを考えると、 作問者はこの(1)の問題では、引き算は用いないと想定しているということが推察されます。 (引き算を用いるということは-の値の範囲が必要になるので8bitだと-128~127です。 128以上の値を取りうる時点で引き算は想定されていません) このことからM-Nとか、N-Mをしてその正負を見るみたいな解法ではないと判断します。 よって足し算を用いた解法を検討します。 このタイミングでレジスタ0のインクリメントという解法に辿り着きました。 条件が多いですが、その条件によって何が排除されるのかを考えるのが、回答に辿り着く近道になります。
(2)は掛け算と引き算の実装が求められます。
まず掛け算はn × Aを実装する場合、add命令をn回ループするという手法を用います。
そして引き算は2の補数表現を利用します。
a-bを実装する場合、ビット反転したbを~bとおくと、a-b = a+(~b)+1で実現可能です。
そのため、ビット反転が必要になります。
ビット反転は、反転したい数字と0xFFとの排他的論理和(XOR)をとることで実現できます。
仮定においてアドレスD1にFFが格納されているのは、ビット反転をさせるためということになります。
これもある意味実装すべき操作のヒントになっていたのかと思います。
また、この問題もロード命令の回数に制限があるので、0の格納にも1-1=0を用いて値の格納をします。
掛け算はFnの値の回数だけ行って、その後mの回数だけその処理を繰り返します。
解答における困難な点はループ処理、掛け算、引き算なのでそこまでアルゴリズムが難しいということはないかと思います。
以下がアルゴリズムの実装のフローです。
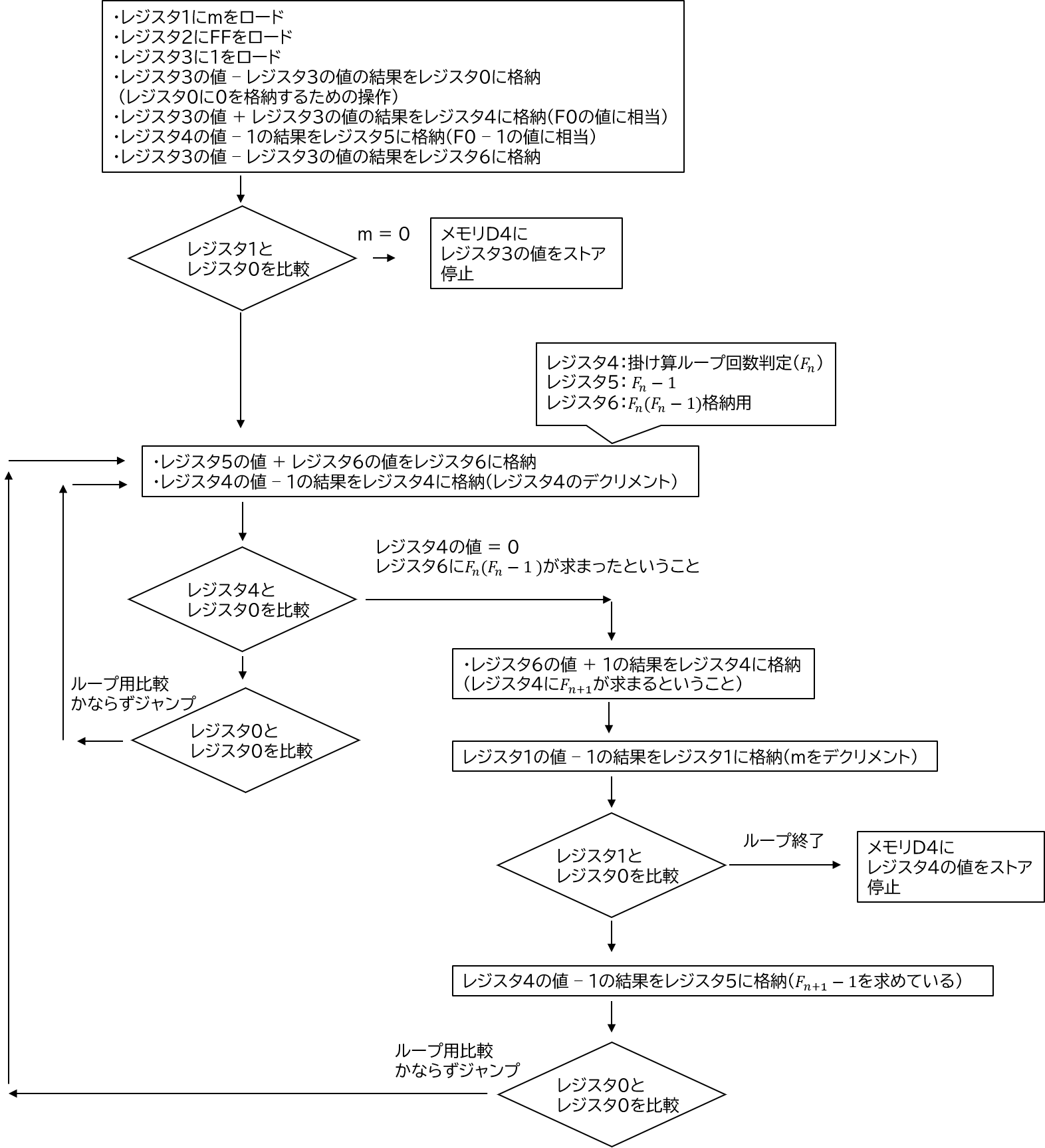
2の補数表現による引き算の実装は抑えてたらかなり勉強してた人の部類に入ると思います。 私にとって2の補数表現なんて、学部の1回か2回に軽く教わって、正直意味わからないままの概念です。 実際の試験においてはまず日本語で実装するアルゴリズムの概要を示しておくのがいいと思います。 そうすれば少々マシン語の記述で実装手順に間違いがあってもいくらかばかし部分点がもらえると思います。
133.3.201.145
どうやらこのipは京大が所有しているipアドレスのひとつのようです。
| EID | Age | Name | Branch | Amount | Hours |
|---|---|---|---|---|---|
| 347 | 25 | Alex | LA | 189000 | 62 |
| 199 | 27 | Sam | NY | 251000 | 67 |
readとwriteのロックの順番がそれぞれのプロセスで逆であることによりデッドロックが発生しています。 以下が修正案です
1: lock "read" semaphore
2: if (list.count() > 10000) {
3: print("too many")
4: }
5: unlock "read" semaphore
6: lock "write" semaphore
7: list.add(new_value)
8: unlock "write" semaphore
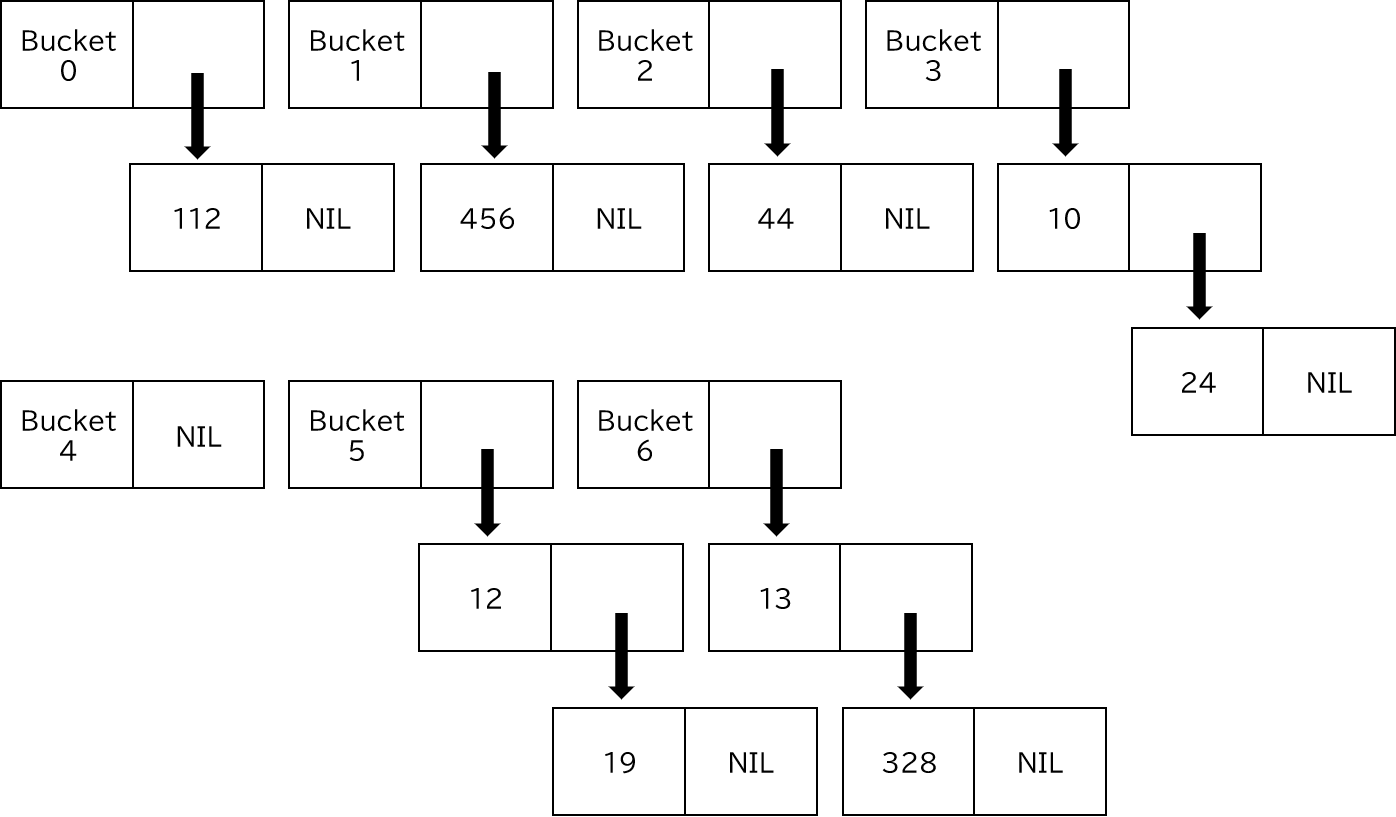
Procedure delete_key(key)
index <- key % 7 # キーを7で割った値を格納
head <- hash_table[index]
if head == null
return # 値がない場合は終了
endif
if head.value == key
hash_table[index] = head.next # ポインタの付け替え
return
endif
prev <- head # ひとつ前のリストのアドレス
curr <- head.next # 値を調べるリストのアドレス
while curr != null
if curr.value == key
prev.next = curr.next # ひとつ前のアドレスの次のポインタを今のリストの次のアドレスに付け替える
return
prev <- head # アドレスの更新
curr <- head.next
endwhile
return # キーが見つからず終了
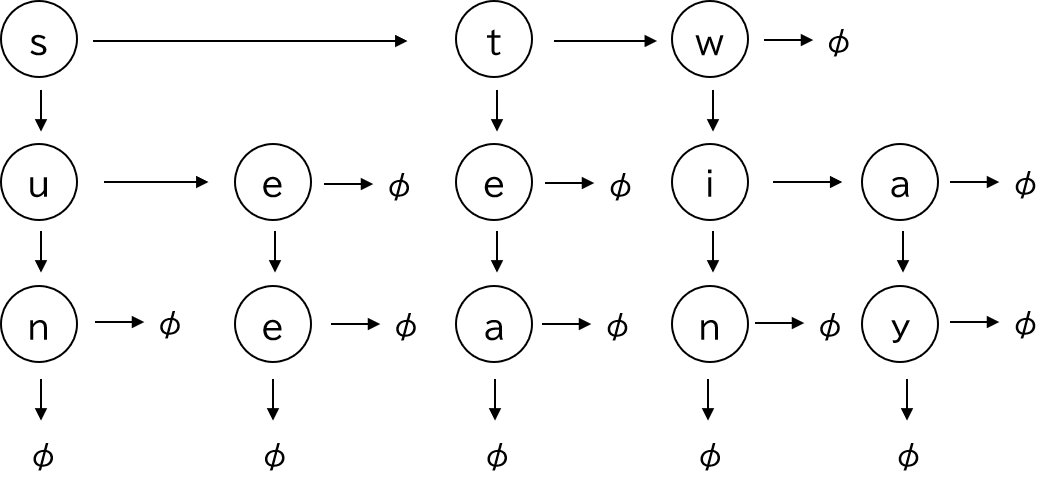
擬似コードにおいて、与えられる引数はwordとnodeとする。 wordは検索するワードであり、nodeは木における一番頂点に当たるノードであるとする。 また、擬似コード内で利用する関数countは文字列の文字数を返す関数であるとする。
Procedure serch_word(node, word)
index <- 0
count <- count(word) # 文字数を格納
while node != null
if node.data == word[index] # 検索している文字の発見
index <- index + 1 # 次の文字を設定
if index == count
return True # 最後まで発見
node <- node.child # 次の子を検索
else
node <- node.sibling # 次の兄弟を検索
return False # 発見できず